ファイナンシャルプランナーの私がご相談を承る分野は、マイホーム計画の進め方、その際の住宅ローン、将来的ライフプランの備えとしての資金準備、生命保険の備え方と多岐な分野に渡りますが、これらご相談の中でリスクへの不安を吐露される事があります。
これらは全てライフプランの充実には大切なこととは解っていても姿かたちが見えません。
それ故に果たして現状の備えや進め方で充分か否かの判断がどうしても手探りとなり、後々失敗や後悔を残さないだろうか?大丈夫だろうか?という不透明な不安が「リスク」という表現で発せられるのではないでしょうか。
他のコラム記事でも何度か触れておりますが、「リスク」という言葉は日常的に「危険」を意味する場面で使われている様に思えますが、ファイナンシャルプラン上のリスクの定義は「不確実性」を指します。
この両者の違いは、完全に「危険」な状態のものは「確実な危険」であり、もはやリスクが高いのでは無く明確に避けるべき対象として分けられます。
それに対し、かなり危険そうだが予見が難しいもの、この不確実性が「リスク」として扱われるのです。
その点では、何もネガティブな事象だけがリスクの対象では無く、「当たり」が出る様なプラス要因も不確実性が伴えばリスクとしてみなす事が出来ます。
当たるか当たらないか分からない状態という事です。
今回はファイナンシャルプランのお話で、リスクのメカニズムについての話題を取り上げます。

⬜︎ リスクの大きさは?
さて、リスクの定義確認したところで、次はリスクの大きさです。
住宅購入の際、住宅ローンを多くの方々が利用しますが、「返済額をここ迄に抑えないとリスクが…」であったり、将来のライフプランを考え銀行の相談窓口で「貯蓄はしたいけど株式投資信託はリスクが…」などといった使われ方は、不確実さへの不安という点で正にリスクの議論なのですが、問題はリスクの大きさをどの様にして測るかです。
この辺りが日頃からリスクに不安を感じ対処を考察する際、あやふやになってはいないでしょうか?
結果としてリスクの評価が「主観的」になってはいないでしょうか?
失敗の不安が大きい物事のリスクが高く感じられ、危険性の認識が低い事柄はリスク感が低い。
この様な状態が主観的に評価している状態です。
しかし、この様に感覚任せで不確実性を評価しようとすれば、その判断は恣意的になり心許ないのはいうまでもありません。
「客観的」方法で不確実さの程度を正確に見抜きたいですね。
⬜︎ リスクの根拠を何に求める?
それではどうすれば主観を排除し客観性を求められるのでしょうか。
リスクをの程度を知った上でそれを生かしたいのは未来ですが、未来の出来事を予知する事は超能力でも宿らなければ適いません。でも過去はどうでしょう?
過去のデータが揃えられる対象であれば、それは全て事実の蓄積です。これ以上のリアルは有りません。
リスクの測定にはこの過去のデータを用います。
根拠を揃える事など適わない将来を想像するのでは無く、過去の履歴から傾向を分析し、その結果を元に将来予測の手掛かりにしようという事です。
どの様な進め方で分析するのか?
そこから何が読み取れるのか?
次はそこを見ていきましょう。
⬜︎ 過去データから何がみえる?
理屈ばかりでは理解しにくいので例を上げます。
数学テストの成績です。(勿論社会科でも何でも良いです)
A君の過去10回のテスト結果は下のグラフです。

勉強しないでお母さんに叱られたA君は「次のテストは数学で80点以上取る!」と大見得を切ります。
それを聞いたお母さんは「またか」と呆れ顔・・・。
確かにそれまでの成績をみれば無理もありません。
皆さんはどう思いますか?
このA君の「可能性」を「数理的」に予想してみてください。
「信じてあげよう!」とか「それは無理じゃない」と励ましやレッテル張りで無くあくまで客観的に!
加えてもう一例。
下のグラフは、先程同様B君とC君の数学の過去8回の成績です。
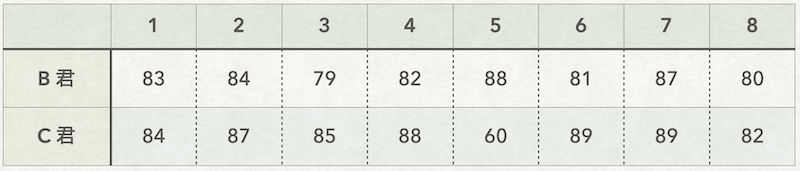
次のテストは80点以上が合格となる場合
この結果から次のテストではB君とC君どちらが合格の可能性が高いかという問題です。
これらの場合、印象では無く数理的に答えを見出そうとすれば、多くの方が「平均点」に着目するのではないでしょうか。
A君の平均点は48点。
公言した80点には全然及びません。
B君C君の平均点も比較してみましょう。
なんと二人とも平均点は83点!全く同じです。
「じゃあ次のテストの可能性もどちらもイーブン?」
いえいえ答えをきちんと出しましょう。
「うーんB君の方が安定している様にも見えるし」
「でもC君は高得点の頻度が多いよ」
アレレ!また印象頼りに戻ってしまいました・・・。
そろそろ答えを出しましょう。
この様に過去の履歴から将来の可能性を推定する場合に便利なのが「標準偏差」です。
⬜︎ データ分析してみよう
それではまず、A君、B君、C君の標準偏差を計算してみましょう。式は、
{(平均点 − 点数1)² +(平均点 − 点数2)²+・・・× (平均点 − 点数n)²} ÷n
これの平方根です。
何だか訳が分からなくなってしまいましたか?シンプルに説明しましょう。
まず、過去全8回テスト結果の点数を一つづつ平均点とどの位乖離し分散しているかを測ります。
そこで8個の(平均点−実点数)を合計し8で割れば、乖離の平均が分かりそうに思えませんか?
でも、これで計算すると平均点よりプラスとマイナスのものが相殺され答えはゼロ、つまり平均点に戻ってしまいます。(試してみて下さい)
そこで(平均点−実点数)を二乗すれば答えは全てプラスになるので平均点と各実点数の「離れ具合」だけを並べる事が出来ます。
そして二乗していたものを最後に平方根で戻せば平均点との乖離幅のみが測定できるという訳です。
この値をσ(シグマ)で表記し、平均値からプラスσとマイナスσの間になる確率は統計学的に68.27%(約2/3)とされています。
例えば平均点50点、σ=5であった場合、45点~55点に収まる確率が約2/3という事になります。
それではこの数式を用いて三人の結果を見てみましょう。

⬜︎ 果たして結果は?
まずはA君です。
A君の過去の平均点数は48点でした。
目標の80点には遠く及びません。
せめて60点は取ってほしいお母さんとしても48点では心配でしょうがありません。
それではA君は頑張ればどの位の見込みが有るのでしょうか?
先の過去8回の点数から計算するとσ=12でした。
という事は48ー12=36、48+12=60ですので、36点~60点に入る可能性が2/3です。
という事は、それ以上、それ以下の確率はそれぞれ(100%ー68.27%)÷ 2なので、60点を取る確率は約16%という事になります。
平均だけ見れば遠い目標も、確率に置き換えれば頑張れば手が届きそうです!
因みに啖呵を切った80点は、
(80ー48)÷12≒2.6σであり、確率的には約0.4%。
ちょっと大風呂敷を広げ過ぎたようにも・・・。
次にB君、C君のσ値をみてみましょう。平均点は二人とも83点でした。
標準偏差はB君σ=3、C君σ=9です。
となるとB君80点~86点、C君74点~92点の確率が約2/3となります。
結果から見るとC君の方が高得点の可能性が高いともいえますが、反面B君より振るわず80点以下の可能性も高く、確実性という点ではB君の方が勝るという予想がなりたちます。
⬜︎ リスクを定量的に評価する場合
実は今回取り上げたリスクの測定方法、標準偏差は多くの方が役立てた経験があるはずなのです。
学生時代に聞き馴染みのある「偏差値」です。
これは平均点との乖離を標準偏差を用いて指数化したものですね。
但し、あくまでも過去の履歴から読み取れる傾向を将来にも当てがい「期待値」を求める機能なので絶対視はできない点の他に、今回は過去8回のデータの元に解説しましたがサンプル数が多ければ多いほど精度が増すが少なければ精度は低下する点(大数の法則といいます)、サンプルの数値は恣意的にバイアスの掛からな正規分布した数集団でない場合も精度が保てない点は注意が必要です。
小難しいお話にお付き合いいただきましたが、身の回りにあるリスクと感じる物事に接する際、感覚的にいたずらに不安を感じたり、不用意に楽観視し対処を誤り失敗のタネとならぬよう、過去の履歴を整理し、判断する事でリスクコントロールの知恵が生まれるはずです。
次回コラムはリスクマネージメントをライフプランの中で活かす方法についてお話いたします。
トップページはこちらから